Konversi Bilangan
Oleh = Mochammad Haldi Widianto
Sistem Bilangan atau Number System adalah Suatu cara untuk mewakili besaran dari suatu item fisik. Sistem Bilangan menggunakan suatu bilangan dasar atau basis (base / radix) yang tertentu. Dalam hubungannya dengan komputer, ada 4 Jenis Sistem Bilangan yang dikenal yaitu : Desimal (Basis 10), Biner (Basis 2), Oktal (Basis 8) dan Hexadesimal (Basis 16). Berikut penjelesan mengenai 4 Sistem Bilangan ini:
Bilangan Desimal
Bilangan desimal adalah bilangan yang paling umum atau paling sering kita temui di kehidupan sehari-hari. Sistem bilangan ini menggunakan basis 10 atau menggunakan 10 macam bilangan yaitu 0, 1, 2, 3, 4, 5, 6, 7, 8, dan 9. Sistem bilangan desimal dapat berupa integer desimal (decimal integer) dan dapat juga berupa pecahan desimal (decimal fraction).
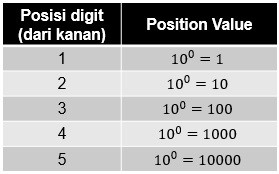

Gambar 1. Tabel Decimal
Bilangan Biner
Bilangan biner (basis 2) adalah sistem bilangan yang hanya terdiri dari 2 simbol yaitu 0 dan 1. Bilangan Biner ini di populerkan oleh John Van Neuman. Contohnya menggunakan bilangan biner agar bisa saling berkomunikasi antara komponen (hardware) maupun antar sesama komputer. Karena komputer hanya menggunakan bahasa mesin, yaitu apabila komputer mendapatkan sinyal listrik bernilai 1, apabila komputer tidak mendapatkan sinyal listrik berarti bernilai 0.


Bilangan Hexadesimal
Bilangan hexadesimal (basis 16). Hexa berarti 6 dan Desimal berarti 10 adalah jenis sistem bilangan yang terdiri dari 16 simbol yaitu: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A(10), B(11), C(12), D(13), E(14), dan F(15). Berbeda dengan ke tiga sistem bilangan yang telah dibahas. Sistem bilangan hexadesimal memadukan 2 unsur yaitu angka dan huruf.
Baca juga: Perkembangan Operating System atau Sistem Operasi
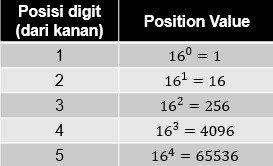
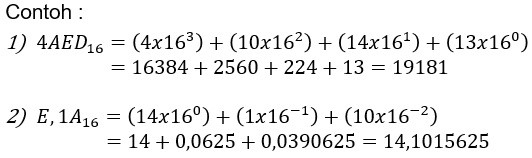
Gambar 3. Hexadecimal
Teknik Konversi Antar Sistem Bilangan
Pemahaman tentang konversi antara sistem bilangan penting untuk berbagai aplikasi dalam komputasi modern. Berikut adalah teknik konversi yang umum digunakan:
A. Konversi Desimal ke Sistem Lain
- Desimal ke Biner: Gunakan metode pembagian berulang dengan 2 dan ambil sisanya dari bawah ke atas.
Contoh: Konversi desimal 13 menjadi biner: 13÷2=6 sisa 113 \div 2 = 6 \, \text{sisa} \, 113÷2=6sisa1 6÷2=3 sisa 06 \div 2 = 3 \, \text{sisa} \, 06÷2=3sisa0 3÷2=1 sisa 13 \div 2 = 1 \, \text{sisa} \, 13÷2=1sisa1 1÷2=0 sisa 11 \div 2 = 0 \, \text{sisa} \, 11÷2=0sisa1
Jadi, 1310=1101213_{10} = 1101_21310=11012. - Desimal ke Oktal: Gunakan metode pembagian berulang dengan 8 dan ambil sisanya dari bawah ke atas.
- Desimal ke Heksadesimal: Gunakan metode pembagian berulang dengan 16 dan ambil sisanya dari bawah ke atas, mengganti angka lebih besar dari 9 dengan huruf A-F.
B. Konversi Biner, Oktal, dan Heksadesimal ke Desimal
Untuk mengkonversi bilangan non-desimal ke desimal, gunakan ekspansi seperti yang ditunjukkan dalam contoh-contoh sebelumnya.
C. Konversi Biner ke Oktal dan Sebaliknya
Biner dan oktal memiliki hubungan yang erat karena 1 oktal setara dengan 3 bit biner. Oleh karena itu, konversi antara keduanya melibatkan pengelompokan bit-bit tersebut dalam kelompok-kelompok 3, dimulai dari kanan.
D. Konversi Biner ke Heksadesimal dan Sebaliknya
Heksadesimal merepresentasikan 1 digit dengan 4 bit biner. Oleh karena itu, konversi antara keduanya melibatkan pengelompokan bit-bit tersebut dalam kelompok-kelompok 4, dimulai dari kanan.
Pentingnya Pemahaman Konversi Sistem Bilangan
Pemahaman yang baik tentang konversi sistem bilangan adalah keterampilan dasar yang diperlukan dalam pemrograman komputer, desain sirkuit digital, dan dalam analisis keamanan informasi. Dengan memahami bagaimana bilangan direpresentasikan dan diubah antara sistem-sistem ini, para profesional teknologi dapat merancang sistem yang efisien, memecahkan masalah kompleks, dan memastikan integritas data. Selain itu, pemahaman ini juga penting dalam memahami dasar-dasar arsitektur komputer dan algoritma.
Referensi:
- http://sistembilangan.blogspot.com/p/materi.html
http://student.blog.dinus.ac.id/manuelsetyo/2018/08/08/sistem-bilangan/


Comments :