Metode K-Maps
Oleh = Mochammad Haldi Widianto
Pengertian K-Map
Karnaugh Map (K-Map) adalah representasi grafis dari tabel kebenaran yang memetakan semua kemungkinan kombinasi input dan output dari sebuah fungsi logika. Peta ini disusun dalam bentuk grid, di mana setiap sel mewakili kombinasi input yang unik. Dengan menandai sel-sel ini sesuai keluaran yang diinginkan, desainer dapat dengan mudah melihat kelompok nilai yang dapat digabungkan untuk menyederhanakan fungsi logika.
K-Map merupakan teknik penyederhanaan fungsi logika dengan cara pemetaan. K-Map terdiri dari kotak-kotak yang jumlahnya sesuai dengan jumlah variabel input dari rangkaian logika yang sedang dihitung. Metode ini efektif digunakan untuk fungsi dengan jumlah variabel maksimal enam; untuk lebih dari itu, disarankan menggunakan perangkat lunak khusus.
Langkah-langkah Pemetaan K-Map
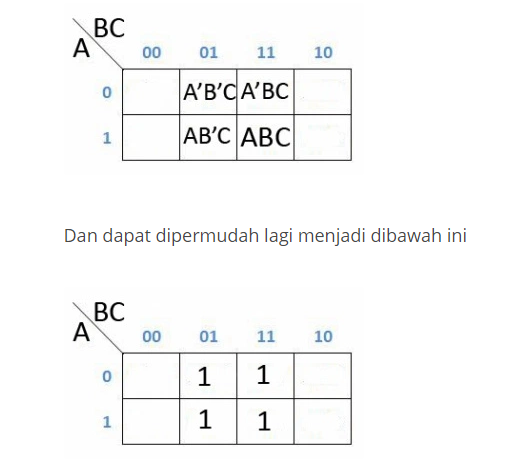
Gambar 1. Penyederhanaan menggunakan K-Maps
- Susun persamaan aljabar Boolean atau buat tabel kebenaran dari fungsi logika yang akan disederhanakan.
- Gambarlah K-Map dengan jumlah sel = 2^jumlah variabel input.
- Isi sel K-Map sesuai dengan nilai output pada tabel kebenaran (1 atau 0).
- Kelompokkan (grouping) sel-sel yang berisi nilai 1 (atau 0 untuk ekspresi POS minimal) dalam kelompok berukuran 2, 4, 8, atau kelipatan dua lainnya. Pengelompokan hanya boleh dilakukan secara horizontal atau vertikal, bukan diagonal.
- Tulis ekspresi logika hasil pengelompokan; setiap kelompok menghasilkan satu suku dalam ekspresi logika yang disederhanakan.
Jenis-jenis K-Map
- K-Map 2 variabel (2×2 kotak)
- K-Map 3 variabel (2×4 kotak)
- K-Map 4 variabel (4×4 kotak)
- K-Map 5 variabel atau lebih (kombinasi beberapa K-Map).
Struktur dan Pembentukan K-Map
Jumlah kotak pada K-Map bergantung pada jumlah variabel input.
Misal:
- 2 variabel: 2^2 = 4 kotak
- 3 variabel: 2^3 = 8 kotak
- 4 variabel: 2^4 = 16 kotak
Contoh format K-Map:
K-Map 2 Variabel:
| AB | 00 | 01 | 11 | 10 |
| f |
K-Map 3 Variabel:
| ABC | 000 | 001 | 011 | 010 | 110 | 111 | 101 | 100 |
| f |
K-Map 4 Variabel:
| ABCD | 0000 | 0001 | 0011 | 0010 | 0110 | 0111 | 0101 | 0100 | 1100 | 1101 | 1111 | 1110 | 1010 | 1011 | 1001 | 1000 |
| f |
Pengisian dan Penyederhanaan K-Map
- Setiap kotak diisi dengan nilai output dari tabel kebenaran.
- Pengelompokan dilakukan pada sel yang berisi 1 (untuk SOP) atau 0 (untuk POS), dengan aturan kelompok berukuran kelipatan dua dan berbentuk persegi atau persegi panjang.
- Setiap kelompok menghasilkan satu suku dalam ekspresi logika yang disederhanakan.
Contoh Penyederhanaan Menggunakan K-Map
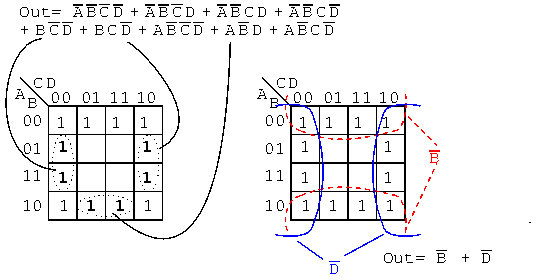
Gambar 2. Penyelesaian menggunakan K-Maps
Contoh K-Map 2 Variabel:
Tabel kebenaran fungsi F(A, B):
| A | B | F |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Langkah-langkah:
- Gambarkan K-Map dan isi nilai dari tabel kebenaran.
- Kelompokkan nilai 1 yang berdekatan.
- Ekspresi logika yang disederhanakan:
F = AB’ + A’B
Contoh K-Map 3 Variabel:
Tabel kebenaran fungsi F(A, B, C):
| A | B | C | F |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Ekspresi logika yang disederhanakan:
F = BC’ + A’B + AC’
Keuntungan dan Keterbatasan K-Map
Keuntungan:
- Memudahkan penyederhanaan ekspresi logika secara visual.
- Mengurangi jumlah gerbang logika dan kompleksitas rangkaian.
- Efisien untuk desain rangkaian digital kecil hingga menengah.
Keterbatasan:
- Tidak efisien untuk fungsi dengan lebih dari 5 atau 6 variabel.
- Penyederhanaan manual menjadi rumit dan rawan kesalahan untuk K-Map besar.
Referensi:
- https://helmifadhiel.wordpress.com/2015/11/16/karnaugh-map-beserta-penjelasannya/
- https://www.google.com/url?sa=i&source=images&cd=&ved=2ahUKEwjogJ3EwsPmAhWJaCsKHewpDmgQjRx6BAgBEAQ&url=https%3A%2F%2Fwww.allaboutcircuits.com%2Ftextbook%2Fdigital%2Fchpt-8%2Flarger-4-variable-karnaugh-maps%2F&psig=AOvVaw3MjDsuiMocmtBqKItP6OxX&ust=1576907009686748


Comments :