Jenis-Jenis Analisis Regresi
Analisis regresi adalah teknik statistik yang digunakan untuk memahami hubungan antara satu atau lebih variabel independen (prediktor) dan variabel dependen (respons). Teknik ini sangat berguna dalam berbagai bidang seperti ekonomi, biologi, teknik, dan ilmu sosial untuk membuat prediksi, mengidentifikasi tren, dan memahami hubungan sebab-akibat. Dalam artikel ini, kita akan membahas berbagai jenis analisis regresi yang umum digunakan, termasuk regresi linier, regresi logistik, regresi Poisson, regresi Ridge, dan regresi LASSO.
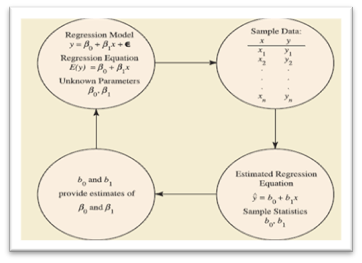
Gambar 1. Proses Estimasi untuk Regresi Linier Sederhana

Gambar 2. Proses Estimasi untuk Regresi Linier Berganda
Jenis-Jenis Analisis Regresi dalam Ilmu Statistik
1. Regresi Linier
Definisi
Regresi linier adalah jenis analisis regresi yang paling sederhana dan paling umum digunakan. Ia berusaha untuk menemukan hubungan linear antara variabel independen (X) dan variabel dependen (Y) melalui persamaan garis lurus: Y=β0+β1X+ϵY = \beta_0 + \beta_1X + \epsilonY=β0+β1X+ϵ, di mana β0\beta_0β0 adalah intercept, β1\beta_1β1 adalah slope, dan ϵ\epsilonϵ adalah error term.
Aplikasi
- Ekonomi: Menentukan hubungan antara pendapatan dan pengeluaran.
- Kesehatan: Mengukur efek obat pada tekanan darah.
- Pemasaran: Memprediksi penjualan berdasarkan pengeluaran iklan.
Keunggulan
- Kesederhanaan: Mudah diinterpretasikan dan diimplementasikan.
- Kecepatan: Cepat dihitung dengan komputasi yang relatif rendah.
Kelemahan
- Asumsi Linearitas: Tidak cocok untuk hubungan yang tidak linear.
- Sensitif terhadap Outlier: Hasil dapat terdistorsi oleh data outlier.
2. Regresi Logistik
Definisi
Regresi logistik digunakan ketika variabel dependen adalah variabel biner (dichotomous). Ia memperkirakan probabilitas kejadian dari suatu peristiwa dengan menggunakan fungsi logistik. Persamaan regresi logistik adalah: log(p1−p)=β0+β1X\log\left(\frac{p}{1-p}\right) = \beta_0 + \beta_1Xlog(1−pp)=β0+β1X, di mana ppp adalah probabilitas kejadian dari peristiwa.
Aplikasi
- Medis: Memprediksi kemungkinan pasien mengidap penyakit tertentu berdasarkan gejala.
- Pemasaran: Menentukan kemungkinan pelanggan membeli produk.
- Kredit: Memprediksi default pembayaran pinjaman oleh nasabah.
Keunggulan
- Probabilitas: Menghasilkan probabilitas kejadian suatu peristiwa.
- Fleksibilitas: Dapat digunakan untuk model klasifikasi.
Kelemahan
- Multikolinearitas: Sensitif terhadap korelasi tinggi antara variabel independen.
- Interpretasi: Koefisien lebih sulit diinterpretasikan dibanding regresi linier.
3. Regresi Poisson
Definisi
Regresi Poisson digunakan untuk memodelkan data count atau hitungan, di mana variabel dependen adalah jumlah kejadian dari suatu peristiwa dalam interval waktu atau ruang tertentu. Modelnya adalah: log(λ)=β0+β1X\log(\lambda) = \beta_0 + \beta_1Xlog(λ)=β0+β1X, di mana λ\lambdaλ adalah rata-rata kejadian.
Aplikasi
- Kesehatan: Menganalisis jumlah kunjungan pasien ke rumah sakit.
- Kriminalitas: Mengukur jumlah kejahatan di area tertentu.
- Ekonomi: Meneliti jumlah kejadian kegagalan mesin dalam pabrik.
Keunggulan
- Hitungan: Cocok untuk data count.
- Non-Negatif: Memastikan prediksi tidak negatif.
Kelemahan
- Overdispersion: Tidak cocok jika varians jauh lebih besar daripada mean.
- Distribusi: Asumsi distribusi Poisson mungkin tidak selalu terpenuhi.
4. Regresi Ridge
Definisi
Regresi Ridge adalah teknik regulasi yang digunakan untuk menganalisis data yang mengalami multikolinearitas. Ia menambahkan penalti terhadap besar koefisien regresi untuk mengurangi overfitting. Modelnya adalah: β=(XTX+λI)−1XTy\beta = (\mathbf{X}^T\mathbf{X} + \lambda \mathbf{I})^{-1}\mathbf{X}^T\mathbf{y}β=(XTX+λI)−1XTy, di mana λ\lambdaλ adalah parameter regulasi.
Aplikasi
- Genomika: Analisis data genetik dengan banyak prediktor.
- Keuangan: Model prediksi harga saham dengan banyak variabel ekonomi.
- Sains Data: Mengurangi overfitting dalam model dengan banyak fitur.
Keunggulan
- Multikolinearitas: Mengurangi masalah multikolinearitas.
- Stabilitas: Menghasilkan model yang lebih stabil dengan variabel berlebih.
Kelemahan
- Bias: Menambahkan bias ke model.
- Pemilihan Parameter: Memerlukan pemilihan nilai λ\lambdaλ yang tepat.
5. Regresi LASSO
Definisi
Regresi LASSO (Least Absolute Shrinkage and Selection Operator) juga merupakan teknik regulasi yang menambahkan penalti terhadap jumlah nilai absolut koefisien regresi. Modelnya adalah: β=argminβ(∥y−Xβ∥22+λ∥β∥1)\beta = \arg\min_{\beta} \left( \| \mathbf{y} – \mathbf{X}\beta \|_2^2 + \lambda \|\beta\|_1 \right)β=argminβ(∥y−Xβ∥22+λ∥β∥1), di mana ∥β∥1\|\beta\|_1∥β∥1 adalah jumlah nilai absolut dari koefisien.
Aplikasi
- Genomika: Memilih subset gen yang signifikan dari data genetik.
- Keuangan: Mengidentifikasi faktor-faktor ekonomi yang penting dalam model prediksi.
- Pemasaran: Menemukan variabel yang paling relevan dalam kampanye iklan.
Keunggulan
- Pemilihan Variabel: Secara otomatis memilih variabel yang penting.
- Sederhana: Menghasilkan model yang lebih sederhana dan lebih mudah diinterpretasikan.
Kelemahan
- Bias: Menambahkan bias ke model.
- Pemilihan Parameter: Memerlukan pemilihan nilai λ\lambdaλ yang tepat.
6. Regresi Multinomial
Definisi
Regresi multinomial digunakan untuk memodelkan variabel dependen yang memiliki lebih dari dua kategori. Ia memperluas regresi logistik untuk memprediksi probabilitas kejadian dari beberapa kategori.
Aplikasi
- Medis: Memprediksi jenis penyakit berdasarkan gejala.
- Pemasaran: Menentukan kategori produk yang akan dibeli pelanggan.
- Politik: Menganalisis pilihan pemilih dalam pemilu dengan lebih dari dua kandidat.
Keunggulan
- Kategori Ganda: Cocok untuk variabel dependen dengan banyak kategori.
- Fleksibilitas: Mengatasi masalah klasifikasi dengan lebih dari dua kelas.
Kelemahan
- Kompleksitas: Lebih kompleks dibanding regresi logistik biner.
- Interaksi: Sulit untuk menginterpretasikan interaksi antara variabel.
7. Regresi Probit
Definisi
Regresi Probit adalah teknik yang mirip dengan regresi logistik tetapi menggunakan fungsi distribusi normal kumulatif untuk memodelkan probabilitas kejadian dari suatu peristiwa.
Aplikasi
- Medis: Memprediksi keberhasilan suatu perawatan medis.
- Ekonomi: Menganalisis keputusan biner seperti pembelian rumah.
- Psikologi: Mempelajari hubungan antara variabel psikologis dan hasil biner.
Keunggulan
- Distribusi Normal: Cocok untuk data yang diasumsikan mengikuti distribusi normal.
- Interprestasi: Memberikan estimasi probabilitas yang lebih halus.
Kelemahan
- Kesulitan Komputasi: Lebih kompleks dan sulit untuk dihitung dibanding regresi logistik.
- Asumsi: Membutuhkan asumsi distribusi normal yang mungkin tidak selalu sesuai.
Berdasarkan jumlah variabel respon, analisis regresi dibagi menjadi 3 jenis, yaitu:
- Univariat: Terdapat satu variabel respon dan satu atau lebih variabel prediktor
- Bivariat: Terdapat dua variabel respon dan satu atau lebih variabel prediktor
- Multivariat: Terdapat tiga atau lebih variabel respon dan satu atau lebih variabel prediktor
Berdasarkan jumlah variabel prediktor, analisis regresi dibagi menjadi 2 jenis, yaitu:
- Linier Sederhana: Terdapat satu variabel prediktor dan satu variabel respon
- Linier Berganda: Terdapat dua atau lebih variabel prediktor dan satu variabel respon
Sumber: Anderson, Sweeney, and Williams (2008), “Statistics for Business and Economics”, Thomson, South-Western


Comments :