Ukuran Pemusatan Data
Pengertian Ukuran Pemusatan Data

Ukuran pemusatan data adalah nilai yang menunjukkan pusat atau kecenderungan sentral dari suatu himpunan data. Nilai ini memberikan representasi yang baik tentang lokasi tengah dari data tersebut. Dalam analisis data, ukuran pemusatan membantu dalam:
- Menyederhanakan Data: Menyediakan ringkasan yang mudah dipahami dari sekumpulan data yang besar.
- Membandingkan Dataset: Memungkinkan perbandingan antara dua atau lebih dataset yang berbeda.
- Menganalisis Pola: Membantu dalam mengidentifikasi pola atau tren dalam data.
Ukuran pemusatan yang paling umum digunakan adalah mean (rata-rata), median, dan mode.
Dalam ilmu statistika terdapat dua ukuran, yaitu ukuran pemusatan dan ukuran penyebaran data. Ukuran pemusatan data yaitu suatu nilai tunggal yang mewakili suatu kumpulan data dan menunjukkan karakteristik dari data tersebut, dan ukuran penyebaran data adalah suatu ukuran untuk mengetahui seberapa jauh penyebaran data dari nilai rata-ratanya. Jenis-jenis ukuran pemusatan data yaitu:
- Mean (rata-rata hitung)
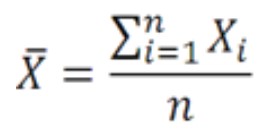
- Median (nilai tengah setelah data diurutkan dari nilai terkecil hingga terbesar)
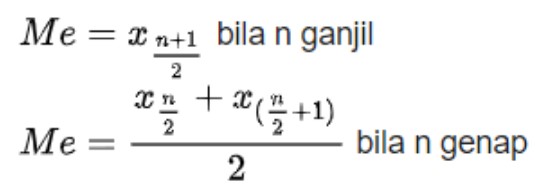
- Modus (nilai yang paling sering muncul atau nilai yang mempunyai frekuensi tertinggi)
- Geometric mean (mengukur laju perubahan variabel dari waktu ke waktu)
![]()
- Geometric mean rate of return (mengukur persentase pengembalian rata-rata dari suatu investasi per periode waktu)
![]()
Kelebihan dan Kelemahan Setiap Ukuran Pemusatan
1. Mean
Kelebihan:
- Menggunakan semua nilai dalam dataset, sehingga memberikan representasi keseluruhan yang baik.
- Mudah dihitung dan digunakan dalam banyak aplikasi statistik.
Kelemahan:
- Sangat sensitif terhadap outliers (nilai ekstrem), yang dapat menyebabkan representasi yang bias.
2. Median
Kelebihan:
- Tidak terpengaruh oleh outliers atau nilai ekstrem, sehingga lebih stabil dalam representasi data yang skewed (condong).
Kelemahan:
- Tidak menggunakan semua nilai dalam dataset sehingga bisa kehilangan informasi penting.
3. Mode
Kelebihan:
- Berguna untuk data kualitatif atau data diskrit di mana rata-rata atau median mungkin tidak masuk akal.
- Menunjukkan nilai yang paling umum atau sering muncul.
Kelemahan:
- Bisa tidak unik atau tidak ada sama sekali dalam dataset.
- Kurang berguna untuk data yang memiliki distribusi yang menyebar dengan nilai yang sama.
Aplikasi Ukuran Pemusatan Data
Ukuran pemusatan data memiliki banyak aplikasi praktis dalam berbagai bidang. Beberapa contohnya meliputi:
1. Analisis Bisnis
Dalam analisis bisnis, mean sering digunakan untuk menghitung kinerja rata-rata, seperti rata-rata penjualan per bulan atau pendapatan per karyawan. Median mungkin lebih relevan dalam konteks distribusi pendapatan atau harga rumah, di mana outliers dapat mempengaruhi mean secara signifikan. Mode dapat digunakan untuk mengidentifikasi produk atau layanan yang paling populer.
2. Pendidikan
Dalam bidang pendidikan, mean dapat digunakan untuk menghitung nilai rata-rata siswa dalam ujian, sementara median mungkin lebih sesuai untuk menganalisis skor tes jika ada beberapa nilai yang sangat rendah atau tinggi. Mode dapat membantu dalam memahami distribusi nilai pada soal tertentu.
3. Kesehatan
Di sektor kesehatan, mean dan median digunakan untuk menganalisis data seperti usia rata-rata pasien atau lama perawatan. Median sering digunakan untuk menganalisis data yang skewed, seperti pengeluaran medis yang sering kali memiliki beberapa nilai yang sangat tinggi.
4. Ekonomi
Dalam ekonomi, mean dan median digunakan untuk menganalisis pendapatan atau distribusi kekayaan. Median pendapatan sering lebih informatif daripada mean, karena pendapatan biasanya skewed oleh beberapa individu dengan pendapatan yang sangat tinggi.
Baca juga: Cara Kerja Data Mining – Seri Data Mining for Business Intelligence (3)
Contoh Perhitungan Ukuran Pemusatan
Mari kita lihat bagaimana menghitung ukuran pemusatan untuk sebuah dataset. Misalnya, kita memiliki dataset yang menunjukkan nilai ujian dari 10 siswa: 72, 85, 90, 65, 88, 75, 95, 60, 80, dan 70.
1. Menghitung Mean:
x‾=72+85+90+65+88+75+95+60+80+7010=78\overline{x} = \frac{72 + 85 + 90 + 65 + 88 + 75 + 95 + 60 + 80 + 70}{10} = 78x=1072+85+90+65+88+75+95+60+80+70=78
2. Menghitung Median:
- Urutkan dataset: 60, 65, 70, 72, 75, 80, 85, 88, 90, 95.
- Karena jumlah nilai genap, median adalah rata-rata dari dua nilai tengah (75 dan 80):
Median=75+802=77.5\text{Median} = \frac{75 + 80}{2} = 77.5Median=275+80=77.5
3. Menghitung Mode:
- Tidak ada nilai yang muncul lebih dari sekali dalam dataset, jadi dataset ini tidak memiliki mode.
Menyimpulkan Ukuran Pemusatan yang Tepat
Memilih ukuran pemusatan yang tepat tergantung pada konteks data dan tujuan analisis. Berikut adalah beberapa panduan umum:
- Gunakan mean ketika data Anda tidak memiliki outliers dan Anda ingin menggunakan semua informasi yang tersedia.
- Gunakan median jika data Anda memiliki outliers atau distribusi yang skewed.
- Gunakan mode untuk data kualitatif atau untuk menemukan nilai yang paling umum dalam dataset.


Comments :