Ukuran Penyebaran Data

Ukuran penyebaran data adalah suatu ukuran yang menyatakan seberapa besar nilai-nilai data berbeda atau bervariasi dengan nilai ukuran pusatnya atau seberapa besar penyimpangan nilai-nilai data dengan nilai pusatnya. Jenis-jenis ukuran penyebaran data antara lain:
1. Rentang (Range)
Definisi
Rentang adalah ukuran penyebaran yang paling sederhana. Rentang dihitung sebagai selisih antara nilai maksimum dan nilai minimum dalam dataset. Secara matematis, rentang dapat dinyatakan dengan formula:
Rentang=Nilai Maksimum−Nilai Minimum\text{Rentang} = \text{Nilai Maksimum} – \text{Nilai Minimum}Rentang=Nilai Maksimum−Nilai Minimum
Kelebihan dan Kekurangan
Kelebihan:
- Sederhana: Rentang mudah dihitung dan dipahami.
- Informasi Dasar: Memberikan gambaran kasar tentang seberapa luas data tersebar.
Kekurangan:
- Sensitif terhadap Outlier: Rentang sangat dipengaruhi oleh nilai ekstrem. Sebuah outlier atau nilai ekstrem dapat secara signifikan memperbesar rentang, sehingga tidak selalu mencerminkan variabilitas data secara akurat.
- Tidak Mengukur Distribusi: Rentang hanya mempertimbangkan dua nilai ekstrem, sehingga tidak memberikan informasi tentang distribusi data di antara nilai-nilai tersebut.
Contoh
Misalkan kita memiliki data berikut tentang tinggi badan (dalam cm) dari 5 orang: 150, 160, 165, 170, 180. Rentangnya adalah:
Rentang=180−150=30 cm\text{Rentang} = 180 – 150 = 30 \text{ cm}Rentang=180−150=30 cm
- Range (selisih antara nilai terbesar dengan nilai terkecil)
![]()
- Varians (ukuran seberapa jauh penyebaran data dari nilai rata-ratanya)
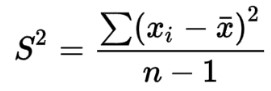
- Standar deviasi (akar dari varians / nilai statistika yang digunakan untuk menentukan bagaimana persebaran data dalam suatu sampel dan melihat seberapa dekat data-data tersebut dengan mean atau rata-rata dari sampel tersebut)

- Coefficient of Variation (CV) adalah suatu sistem perbandingan antara standar deviasi dengan nilai rata-rata yang dinyatakan dalam bentuk persentase
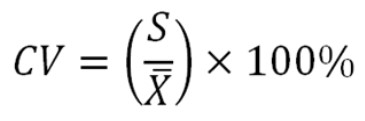
2. Varians (Variance)
Definisi
Varians mengukur seberapa jauh nilai-nilai dalam dataset tersebar dari rata-ratanya. Varians adalah rata-rata dari kuadrat deviasi setiap nilai dari rata-rata. Secara matematis, varians dapat dinyatakan dengan formula:
Varians(σ2)=1N∑i=1N(xi−xˉ)2\text{Varians} (\sigma^2) = \frac{1}{N} \sum_{i=1}^{N} (x_i – \bar{x})^2Varians(σ2)=N1∑i=1N(xi−xˉ)2
di mana xˉ\bar{x}xˉ adalah rata-rata, xix_ixi adalah nilai data, dan NNN adalah jumlah data.
Kelebihan dan Kekurangan
Kelebihan:
- Mengukur Variabilitas: Varians memberikan ukuran yang lebih detail tentang variabilitas data dibandingkan rentang.
- Matematis Kuat: Varians merupakan dasar bagi banyak teknik statistik dan analisis.
Kekurangan:
- Unit Kuadrat: Varians dihitung dalam unit kuadrat dari data, yang mungkin sulit untuk diinterpretasikan dalam konteks praktis.
- Kebutuhan Terhadap Data Lengkap: Varians memerlukan seluruh dataset untuk perhitungan yang akurat.
Contoh
Misalkan kita memiliki data berikut: 4, 8, 6, 5, 7. Langkah pertama adalah menghitung rata-rata:
xˉ=4+8+6+5+75=6\bar{x} = \frac{4 + 8 + 6 + 5 + 7}{5} = 6xˉ=54+8+6+5+7=6
Kemudian, kita hitung varians:
σ2=(4−6)2+(8−6)2+(6−6)2+(5−6)2+(7−6)25=4+4+0+1+15=2\sigma^2 = \frac{(4-6)^2 + (8-6)^2 + (6-6)^2 + (5-6)^2 + (7-6)^2}{5} = \frac{4 + 4 + 0 + 1 + 1}{5} = 2σ2=5(4−6)2+(8−6)2+(6−6)2+(5−6)2+(7−6)2=54+4+0+1+1=2
3. Deviasi Standar (Standard Deviation)
Definisi
Deviasi standar adalah ukuran penyebaran yang paling umum digunakan dan merupakan akar kuadrat dari varians. Deviasi standar memberikan ukuran seberapa jauh nilai-nilai dalam dataset cenderung menyimpang dari rata-ratanya. Secara matematis, deviasi standar dapat dinyatakan dengan formula:
Deviasi Standar(σ)=1N∑i=1N(xi−xˉ)2\text{Deviasi Standar} (\sigma) = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (x_i – \bar{x})^2}Deviasi Standar(σ)=N1∑i=1N(xi−xˉ)2
Kelebihan dan Kekurangan
Kelebihan:
- Unit yang Sama: Deviasi standar dihitung dalam unit yang sama dengan data, sehingga lebih mudah untuk diinterpretasikan.
- Informasi Lengkap: Menyediakan informasi yang lebih komprehensif tentang penyebaran data dibandingkan dengan rentang.
Kekurangan:
- Sensitif terhadap Outlier: Sama seperti varians, deviasi standar dapat dipengaruhi oleh nilai ekstrim.
Contoh
Menggunakan contoh data yang sama dengan perhitungan varians di atas, deviasi standar adalah:
σ=2≈1.41\sigma = \sqrt{2} \approx 1.41σ=2≈1.41
4. Koefisien Variasi (Coefficient of Variation)
Definisi
Koefisien variasi adalah ukuran penyebaran yang dinyatakan dalam bentuk persentase dari rata-rata. Koefisien variasi memberikan gambaran tentang variabilitas relatif dari data, yang memudahkan perbandingan antara dataset dengan skala yang berbeda. Secara matematis, koefisien variasi dapat dinyatakan dengan formula:
Koefisien Variasi(CV)=σxˉ×100%\text{Koefisien Variasi} (\text{CV}) = \frac{\sigma}{\bar{x}} \times 100\%Koefisien Variasi(CV)=xˉσ×100%
di mana σ\sigmaσ adalah deviasi standar dan xˉ\bar{x}xˉ adalah rata-rata.
Kelebihan dan Kekurangan
Kelebihan:
- Perbandingan Relatif: Memungkinkan perbandingan variabilitas antara dataset dengan skala atau unit yang berbeda.
- Persentase: Mudah untuk diinterpretasikan dalam bentuk persentase.
Kekurangan:
- Memerlukan Rata-Rata: Koefisien variasi hanya relevan jika rata-rata data tidak nol, karena dapat memberikan hasil yang tidak bermakna jika rata-rata mendekati nol.
Contoh
Untuk data yang sama (4, 8, 6, 5, 7) dengan deviasi standar 1.41 dan rata-rata 6:
CV=1.416×100%≈23.5%\text{CV} = \frac{1.41}{6} \times 100\% \approx 23.5\%CV=61.41×100%≈23.5%
5. Jangkauan Interkuartil (Interquartile Range – IQR)
Definisi
Jangkauan interkuartil (IQR) mengukur penyebaran data dengan mengabaikan nilai ekstrim. IQR dihitung sebagai selisih antara kuartil ketiga (Q3) dan kuartil pertama (Q1). IQR memberikan ukuran penyebaran yang lebih robust terhadap outlier dibandingkan dengan rentang.
Kelebihan dan Kekurangan
Kelebihan:
- Robust terhadap Outlier: Tidak terpengaruh oleh nilai ekstrim di luar kuartil.
- Mengukur Variabilitas Tengah: Memberikan informasi tentang penyebaran data di sekitar median.
Kekurangan:
- Tidak Mengukur Variabilitas Penuh: Hanya mempertimbangkan bagian tengah distribusi data, sehingga tidak mencerminkan penyebaran data di seluruh rentang.
Contoh
Misalkan kita memiliki data berikut: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20. Kuartil pertama (Q1) adalah 4, dan kuartil ketiga (Q3) adalah 16. Maka:
IQR=Q3−Q1=16−4=12\text{IQR} = Q3 – Q1 = 16 – 4 = 12 IQR=Q3−Q1=16−4=12
6. Box Plot dan Penyebaran Data
Definisi
Box plot adalah alat visual yang digunakan untuk menggambarkan ukuran penyebaran data, termasuk median, kuartil, dan nilai ekstrim. Box plot memberikan gambaran tentang distribusi data dan penyebarannya, serta membantu dalam mengidentifikasi outlier.
Kelebihan dan Kekurangan
Kelebihan:
- Visualisasi: Memberikan gambaran visual yang jelas tentang distribusi data.
- Identifikasi Outlier: Memudahkan identifikasi nilai-nilai ekstrim atau outlier.
Kekurangan:
- Kurang Detail: Tidak memberikan informasi rinci tentang penyebaran data di antara kuartil.
Baca Juga: Analisis Nonparametrik
Contoh
Dalam box plot, box menunjukkan rentang interkuartil, dengan garis di dalam box menunjukkan median. Garis atau “whiskers” menunjukkan jangkauan data di luar kuartil, sementara titik-titik di luar whiskers menunjukkan outlier.


Comments :